Strona GłównaBlogi / marand's blog / Artefakty przy dopasowywaniu transformacji
Artefakty przy dopasowywaniu transformacji
Wielce tajemnicze kształty map niedopasowania mają proste wytłumaczenie przyczyn.
Ladnie dopasowany obrazek wygląda tak:
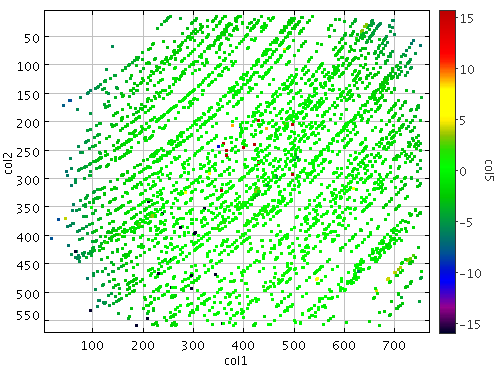
Uzyskujemy taki efekt gdy znalezione przez nas współrzędne środka obrazka są prawidłowe.
Jeśli popsujemy te współrzędne w r.a. to dostaniemy pośladki we współrzędnych r.a. W tym przypadku zmiana wyniosła 1 stopień.
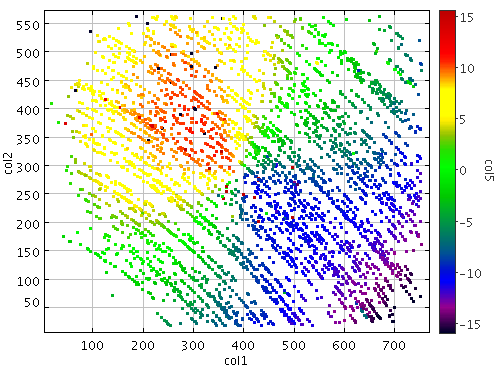
Gdy współrzędne popsujemy w deklinacji ro dostaniemy coś podobnego ale w deklinacji.
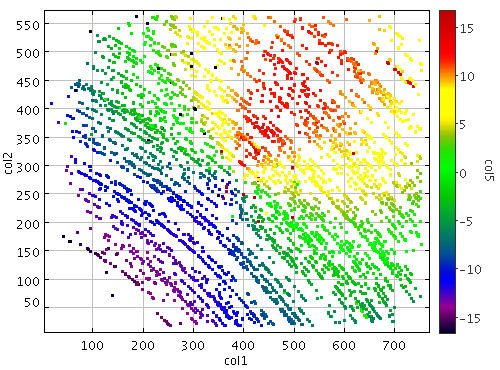
Ciekawe że jest różnica w wyglądzie między tymi dwoma przypadkami.
Można popsuć współrzędne w obu osiach. Wówczas "rowek" pośladków nachyli sie w stosunku do osi r.a.-dec.
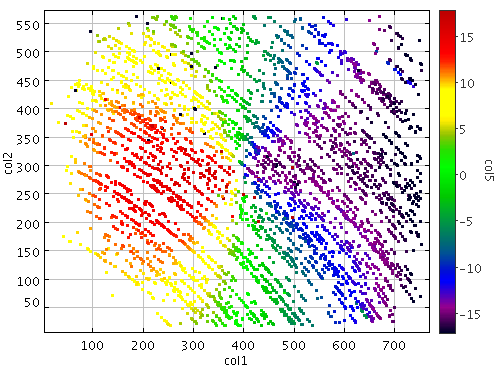
To co tu widać to czysta postać efektu. przy dopasowywaniu płaszczyzn wynik potrafi wyjść bardziej złożony i niesymetryczny.
Zatem nic prostszego - chcemy mieć dobre dopasowanie, musimy poznać środek. Metoda którą się do tego stosuje to iteracyjne liczenie siatki dla pewnych współrzędnych środka i ponownym wyznaczaniu ich na podstawie właśnie dopasowanej funkcji...
Niestety nie jest to prawda. To że dostajemy błędny środek może wywołać zaledwie kilka błędnych pomiarów na 1000 użytych do fitowania. Jeśli w próbkę dostanie się taki dywersant, to zaczynamy szukać środka na podstawie siatki wyglądającej jak pośladki. Mimo kolejnych iteracji wcale nie zbliżamy się do celu tylko błądzimy bo rowku. ;)
Kluczem do uzyskania dobrej siatki jest filtrowanie danych wejściowych. jeśli choć jeden lewy punkt przejdzie przez sito, dopasowanie wyjdzie złe a wszystkie współrzędne obarczone dużym błędem.
- marand's blog
- Zaloguj się by odpowiadać

1. Z tego co pamietam nie ma problemu z dopasowaniem siatki na srodku. Dobrze pamietam?
Jesli tak jest to fitowalbym siatke iteracyjnie, t.j. w kazdym kroku powiekszal jej obszar i odrzucal wadliwe punkty przed nastepnym krokiem. Mozna o nich nie zapominac i fitowac rowniez do nastepnego modelu / ostatecznego modelu.
2. Inna metoda, bardziej czasochlonna, to zonglowanie zestawem punktow az sie znajdzie ten wlasciwy, ktory sie zbiegnie i bedzie "gladki". Co wiecej przy takiej ilosci punktow mozna zonglowac ich rownomiernie rozlozonym podzbiorem co powinno przyspieszyc zbieznosc.
Kamil
Metodę 1 stosuję do szukania środka choć ma dwie wady. Po pierwsze ogranicza się znacznie ilość gwiazd do fitu na potrzeby szukania środka. Po drugie, problem fałszywych gwiazd jest taki sam jak dla całego obrazkam z tym że przy małej ilości gwiazd wystarczy jedna fałszywka by się posypało. Gdy coś się sypnie to wybranie gwiazdy do odrzucenia w cale nie jest takie proste bo gdy fit wykręci się za mocno to nie ona staje się tą najbardziej odstającą. wszystko zależy jak bardzo odstaje od reszty i w którym miejscu. Aktualnie mam trochę dziwną iterację, bo wariancji. licze wariancję i odwalam odstające ponad 3 sigma i tak parę razy. w każdym kroku zbliżam się bardziej do dobrych danych ale 3 sigma nie pozwala by utracić zbyt wiele dobrych. Obecnie tylko dla dwóch kamer licząc tą metodą wychodzą pośladki. Przy czym dla jednej to mam podejrzenia że to jednak wina optyki, bo co bym nie zrobił to dołek jest w tym samym miejscu.
Metoda druga chodzi mi od jakiegoś czasu po głowie ale nie chciało mi się jej zaprogramować. W pewnym sensie jest ona stosowana ale nic nie losuję, to natura sama losuje. Otóż podczas szukania i identyfikacji wyznaczam centra widzenia. Licząc globalną siatkę jako współrzędne środka wspólne dla wszystkich obrazków wybieram medianę z uzyskanych pozycji z każdego obrazka. Z doświadczenia dobre współrzędne zwykle różnią się od tej mediany o nie więcej jak stopień. Mimo to ten stopień sporo zmienia co widać powyżej.